ChebyshevExpander

Hamiltonian

\(H = -\mu\sum_{\mathbf{i}}c_{\mathbf{i}}^{\dagger}c_{\mathbf{i}} + t\sum_{\langle \mathbf{i}\mathbf{j}\rangle}c_{\mathbf{i}}^{\dagger}c_{\mathbf{j}}\)

Code

#include "TBTK/Property/DOS.h"
#include "TBTK/PropertyExtractor/ChebyshevExpander.h"
#include "TBTK/Smooth.h"
#include "TBTK/Solver/ChebyshevExpander.h"
#include "TBTK/TBTK.h"
#include "TBTK/Visualization/MatPlotLib/Plotter.h"
 
#include <complex>
 
using namespace std;
using namespace TBTK;
using namespace Visualization::MatPlotLib;
 
complex<double> i(0, 1);
 
int main(){
    //Initialize TBTK.
    Initialize();
 
    //Parameters.
    const unsigned int SIZE_X = 40;
    const unsigned int SIZE_Y = 40;
    const double t = -1;
    const double mu = 0;
 
    //Set up the Model.
    Model model;
    for(unsigned int x = 0; x < SIZE_X; x++){
        for(unsigned int y = 0; y < SIZE_Y; y++){
            if(x+1 < SIZE_X){
                model << HoppingAmplitude(
                    t,
                    {x+1, y},
                    {x, y}
                ) + HC;
            }
            if(y+1 < SIZE_Y){
                model << HoppingAmplitude(
                    t,
                    {x, y+1},
                    {x, y}
                ) + HC;
            }
        }
    }
    model.construct();
    model.setChemicalPotential(mu);
 
    //Set up the Solver.
    const double SCALE_FACTOR = 5;
    const unsigned int NUM_COEFFICIENTS = 500;
    Solver::ChebyshevExpander solver;
    solver.setModel(model);
    solver.setScaleFactor(SCALE_FACTOR);
    solver.setNumCoefficients(NUM_COEFFICIENTS);
    solver.setCalculateCoefficientsOnGPU(false);
    solver.setGenerateGreensFunctionsOnGPU(false);
    solver.setUseLookupTable(true);
 
    //Set up the PropertyExtractor.
    const unsigned int ENERGY_RESOLUTION = 1000;
    PropertyExtractor::ChebyshevExpander propertyExtractor(solver);
    propertyExtractor.setEnergyWindow(
        -SCALE_FACTOR*0.99,
        SCALE_FACTOR*0.99,
        ENERGY_RESOLUTION
    );
 
    //Calculate the local density of states(LDOS).
    Property::LDOS ldos = propertyExtractor.calculateLDOS({{_a_, _a_}});
 
    //Plot the LDOS.
    Plotter plotter;
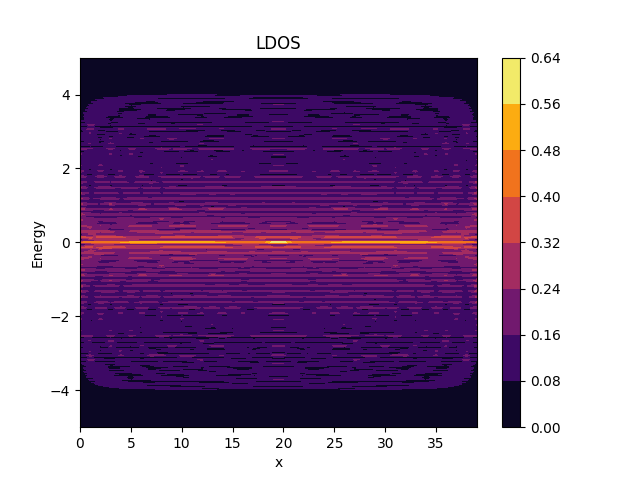
    plotter.plot({_a_, SIZE_Y/2}, ldos);
    plotter.save("figures/LDOS.png");
}

Output