Magnetic impurity (Yu-Shiba-Rusinov)

Hamiltonian

\begin{eqnarray*} H &=& \sum_{\mathbf{i}\sigma}\left(\left(\delta_{\mathbf{i}\mathbf{I}}J\left(\sigma_z\right)_{\sigma\sigma} - \mu\right)c_{\mathbf{i}\sigma}^{\dagger}c_{\mathbf{i}\sigma} - \left(\delta_{\mathbf{i}\mathbf{I}}J\left(\sigma_{z}\right)_{\sigma\sigma} - \mu\right)c_{\mathbf{i}\sigma}c_{\mathbf{i}\sigma}^{\dagger}\right)\\ &+& t\sum_{\langle\mathbf{i}\mathbf{j}\rangle\sigma}\left(c_{\mathbf{i}\sigma}^{\dagger}c_{\mathbf{j}\sigma} - c_{\mathbf{i}\sigma}c_{\mathbf{j}\sigma}^{\dagger}\right)\\ &+& \sum_{\mathbf{i}}\left(\Delta c_{\mathbf{i}\uparrow}c_{\mathbf{i}\downarrow} - \Delta c_{\mathbf{i}\downarrow}c_{\mathbf{i}\uparrow} + H.c.\right), \end{eqnarray*}

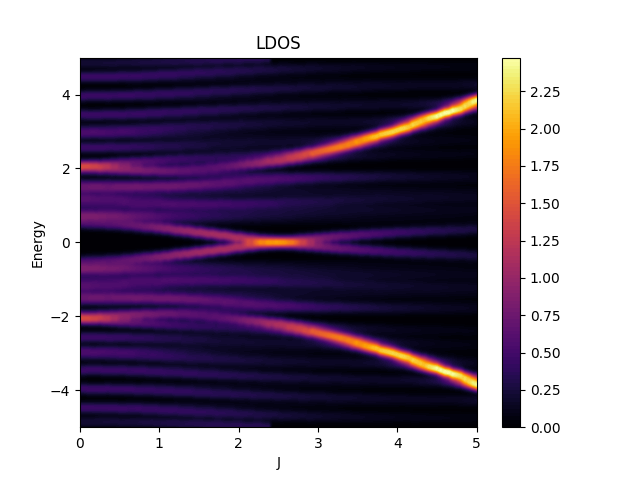
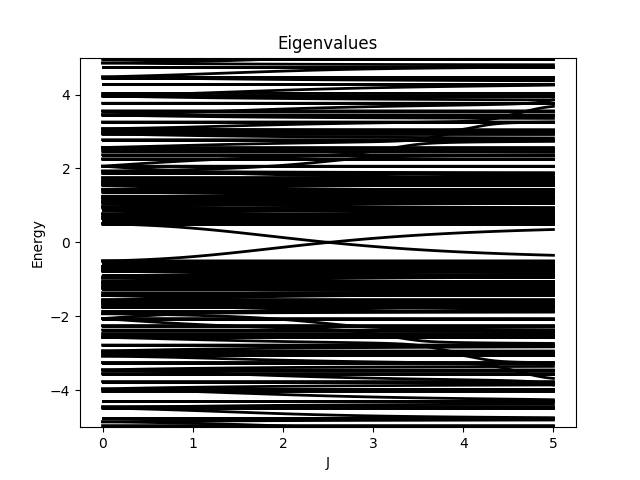
where \(\mathbf{I}\) is the impurity site.

Code

#include "TBTK/Property/DOS.h"
#include "TBTK/PropertyExtractor/Diagonalizer.h"
#include "TBTK/Range.h"
#include "TBTK/Smooth.h"
#include "TBTK/Solver/Diagonalizer.h"
#include "TBTK/TBTK.h"
#include "TBTK/Visualization/MatPlotLib/Plotter.h"

#include <complex>

using namespace std;
using namespace TBTK;
using namespace Visualization::MatPlotLib;

complex<double> i(0, 1);

//Callback that allows for the Zeeman term (J) to be updated after the Model
//has been set up.
class JCallback : public HoppingAmplitude::AmplitudeCallback{
public:
    //Function that returns the HoppingAmplitude value for the given
    //Indices. The to- and from-Indices are indentical in this example.
    complex<double> getHoppingAmplitude(
        const Index &to,
        const Index &from
    ) const{
        Subindex spin = from[2];
        Subindex particleHole = from[3];

        return J*(1. - 2*spin)*(1. - 2*particleHole);
    }

    //Set the value for J.
    void setJ(complex<double> J){
        this->J = J;
    }
private:
    complex<double> J;
};

int main(){
    //Initialize TBTK.
    Initialize();

    //Parameters.
    const unsigned int SIZE_X = 11;
    const unsigned int SIZE_Y = 11;
    const double t = -1;
    const double mu = -2;
    const double Delta = 0.5;

    //Create a callback that returns the Zeeman term and that will be used
    //as input to the Model.
    JCallback jCallback;

    //Set up the Model.
    Model model;
    for(unsigned int x = 0; x < SIZE_X; x++){
        for(unsigned int y = 0; y < SIZE_Y; y++){
            for(unsigned int spin = 0; spin < 2; spin++){
                for(unsigned int ph = 0; ph < 2; ph++){
                    model << HoppingAmplitude(
                        -mu*(1. - 2*ph),
                        {x, y, spin, ph},
                        {x, y, spin, ph}
                    );

                    if(x+1 < SIZE_X){
                        model << HoppingAmplitude(
                            t*(1. - 2*ph),
                            {x+1, y, spin, ph},
                            {x, y, spin, ph}
                        ) + HC;
                    }
                    if(y+1 < SIZE_Y){
                        model << HoppingAmplitude(
                            t*(1. - 2*ph),
                            {x, y+1, spin, ph},
                            {x, y, spin, ph}
                        ) + HC;
                    }
                }

                model << HoppingAmplitude(
                    Delta*(1. - 2*spin),
                    {x, y, spin, 0},
                    {x, y, (spin+1)%2, 1}
                ) + HC;
            }
        }
    }
    for(unsigned int spin = 0; spin < 2; spin++){
        for(unsigned int ph = 0; ph < 2; ph++){
            model << HoppingAmplitude(
                jCallback,
                {SIZE_X/2, SIZE_Y/2, spin, ph},
                {SIZE_X/2, SIZE_Y/2, spin, ph}
            );
        }
    }
    model.construct();

    //Number of iterations.
    const unsigned int NUM_ITERATIONS = 100;

    //Arrays where the results are stored after each iteration.
    Array<double> totalLdos({NUM_ITERATIONS, 500}, 0);
    Array<double> totalEigenValues({
        NUM_ITERATIONS,
        (unsigned int)model.getBasisSize()
    });

    //Iterate over 100 values for J.
    Range j(0, 5, NUM_ITERATIONS);
    for(unsigned int n = 0; n < NUM_ITERATIONS; n++){
        //Update the callback with the current value of J.
        jCallback.setJ(j[n]);

        //Set up the Solver.
        Solver::Diagonalizer solver;
        solver.setModel(model);
        solver.run();

        //Set up the PropertyExtractor.
        PropertyExtractor::Diagonalizer propertyExtractor(solver);

        //Calculate the eigenvalues.
        Property::EigenValues eigenValues
            = propertyExtractor.getEigenValues();

        //Calculate the local density of states (LDOS).
        const double LOWER_BOUND = -5;
        const double UPPER_BOUND = 5;
        const unsigned int RESOLUTION = 500;
        propertyExtractor.setEnergyWindow(
            LOWER_BOUND,
            UPPER_BOUND,
            RESOLUTION
        );
        Property::LDOS ldos = propertyExtractor.calculateLDOS({
            {SIZE_X/2, SIZE_Y/2, IDX_SUM_ALL, IDX_SUM_ALL},
            {SIZE_X/4, SIZE_Y/4, IDX_SUM_ALL, IDX_SUM_ALL}
        });

        //Smooth the LDOS.
        const double SMOOTHING_SIGMA = 0.1;
        const unsigned int SMOOTHING_WINDOW = 51;
        ldos = Smooth::gaussian(
            ldos,
            SMOOTHING_SIGMA,
            SMOOTHING_WINDOW
        );

        //Store the LDOS in totalLdos.
        for(unsigned int e = 0; e < ldos.getResolution(); e++){
            totalLdos[{n, e}] = ldos(
                {
                    SIZE_X/2,
                    SIZE_Y/2,
                    IDX_SUM_ALL,
                    IDX_SUM_ALL
                },
                e
            );
        }

        //Store the eigenvalues in totalEigenValues
        for(unsigned int e = 0; e < eigenValues.getSize(); e++)
            totalEigenValues[{n, e}] = eigenValues(e);
    }

    //Plot the LDOS.
    Plotter plotter;
    plotter.setNumContours(100);
    plotter.setAxes({
        {0, {0, 5}},
        {1, {-5, 5}},
    });
    plotter.setTitle("LDOS");
    plotter.setLabelX("J");
    plotter.setLabelY("Energy");
    plotter.setBoundsY(-5, 5);
    plotter.plot(totalLdos);
    plotter.save("figures/LDOS.png");

    //Plot the eigenvalues.
    plotter.clear();
    plotter.setTitle("Eigenvalues");
    plotter.setLabelX("J");
    plotter.setLabelY("Energy");
    plotter.setAxes({
        {0, {0, 5}},
        {1, {-5, 5}}
    });
    plotter.setBoundsY(-5, 5);
    for(unsigned int e = 0; e < (unsigned int)model.getBasisSize(); e++){
        plotter.plot(
            totalEigenValues.getSlice({_a_, e}),
            {{"color", "black"}, {"linestyle", "-"}}
        );
    }
    plotter.save("figures/EigenValues.png");
}

Output