 |
TBTK
|
Need a break? Support the development by playing Polarity Puzzles |
 |
TBTK
|
Need a break? Support the development by playing Polarity Puzzles |

TBTK is an open-source C++ framework for modeling and solving problems formulated using the language of second quantization. It can be used to set up general models with little effort and provides a variety of native solution methods.
To get started, see the installation instructions, manual, examples, and tutorials. Also, see the blog posts and other resources collected on second-tech.com.
Download TBTK from GitHub. See the installation instructions to make sure you checkout the right version before installation.
Superconductivity 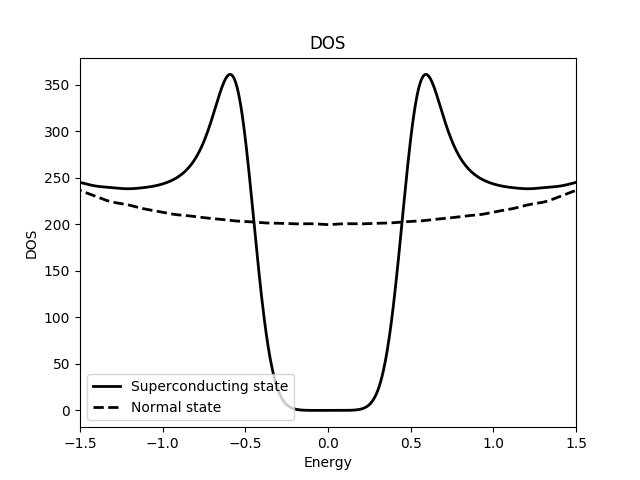 | Caroli-de Gennes-Matricon 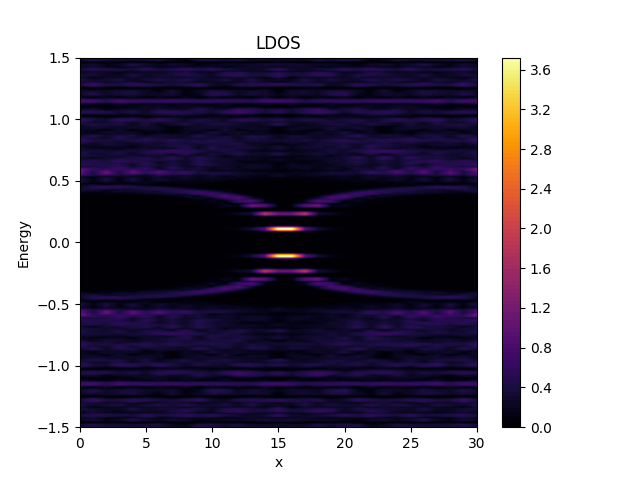 | Magnetism 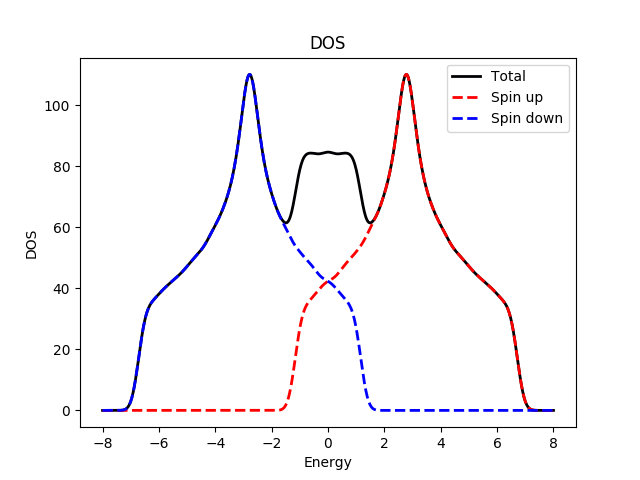 |
Kitaev model 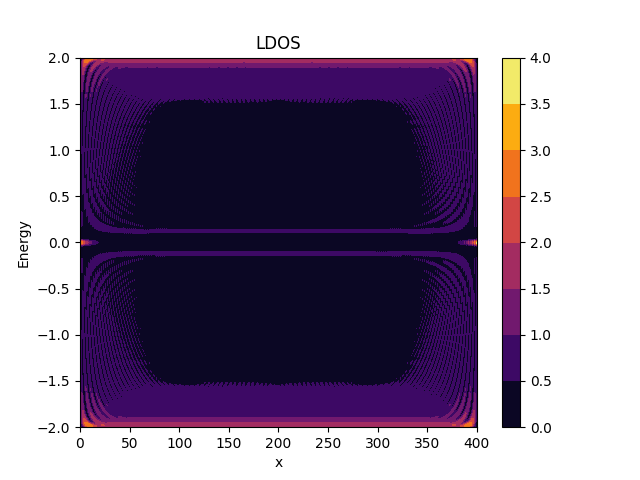 | Anderson disorder 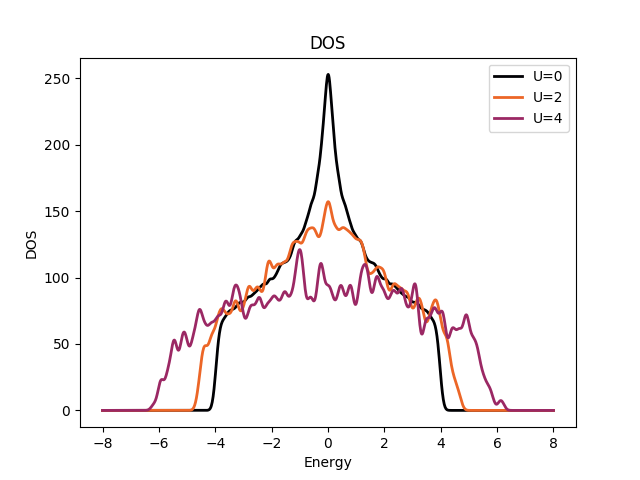 | Yu-Shiba-Rusinov 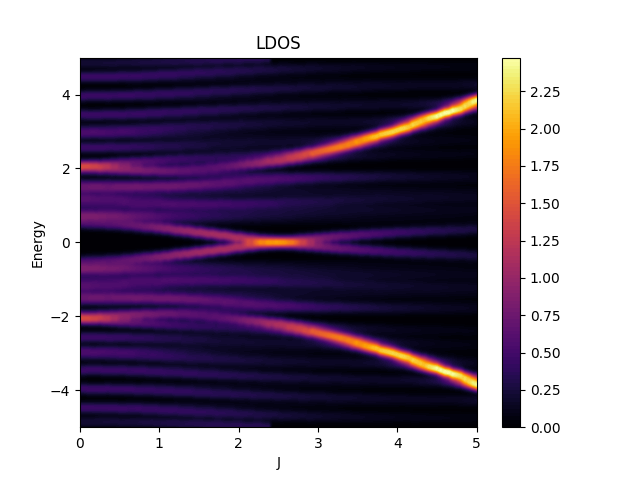 |