Start Page

Welcome to the documentation for TBTK!

TBTK is an open-source C++ framework for modeling and solving problems formulated using the language of second quantization. It can be used to set up general models with little effort and provides a variety of native solution methods.

To get started, see the installation instructions, manual, examples, and tutorials. Also, see the blog posts and other resources collected on second-tech.com.

Download TBTK

Download TBTK from GitHub. See the installation instructions to make sure you checkout the right version before installation.

Core strengths

• The speed of a low-level language with the syntax of a high-level language.
• Results in readable code that puts emphasis on the physics.
• Allows for a wide variety of models and solution methods to be combined in different ways.
• Focus on your own task, while still benefiting from the work of others.
• Gives method developers complete freedom to optimize their solvers without having to worry about model-specific details.
• A versioning system that ensures that results are reproducible forever.

Native production-ready solvers

• Diagonalization
• Block diagonalization
• Arnoldi iteration
• Chebyshev expansion

Examples

Superconductivity	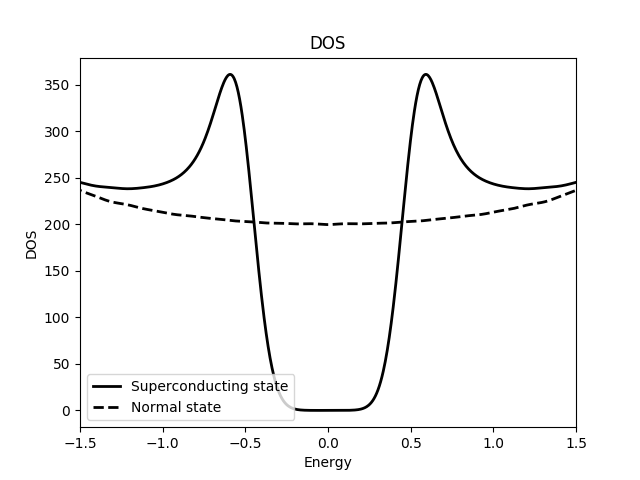Caroli-de Gennes-Matricon	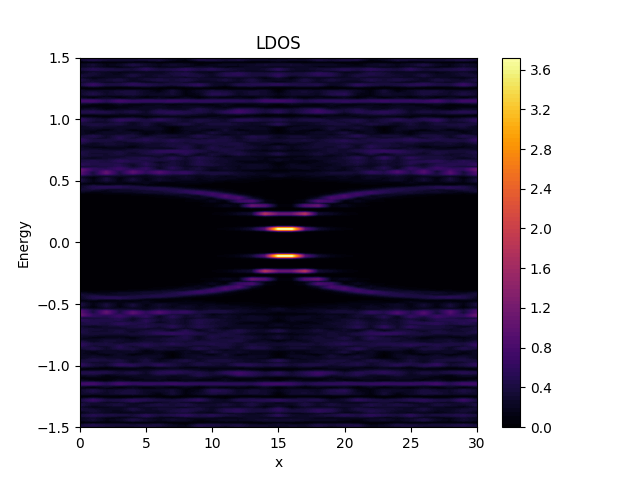Magnetism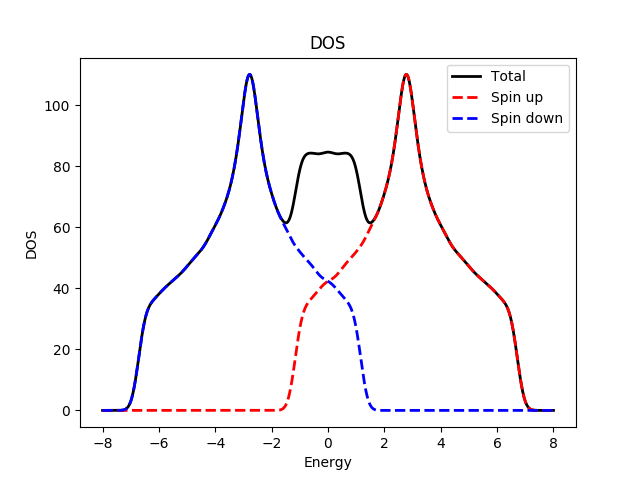
Kitaev model	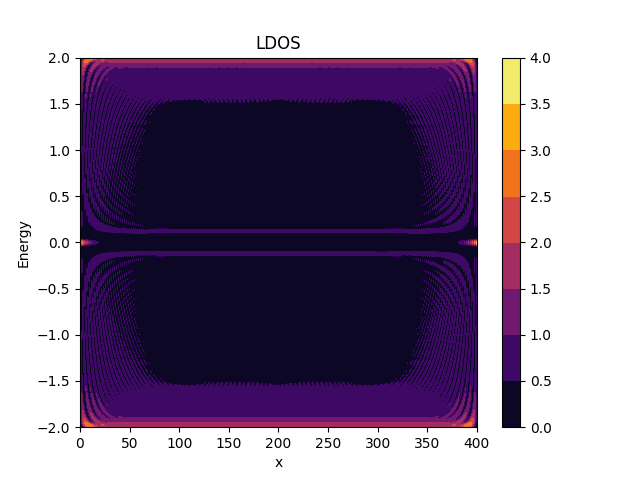Anderson disorder	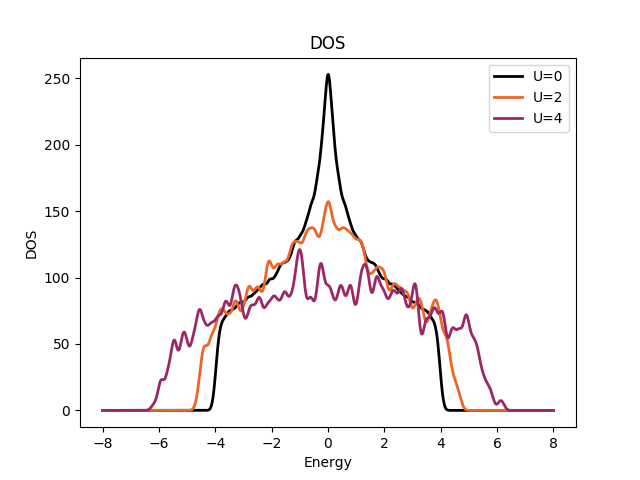Yu-Shiba-Rusinov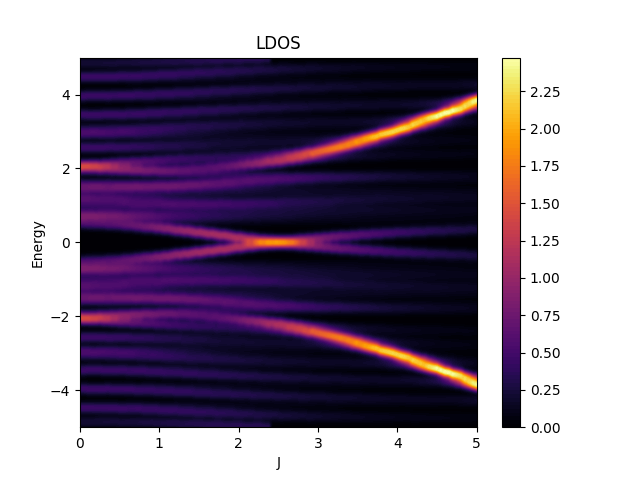